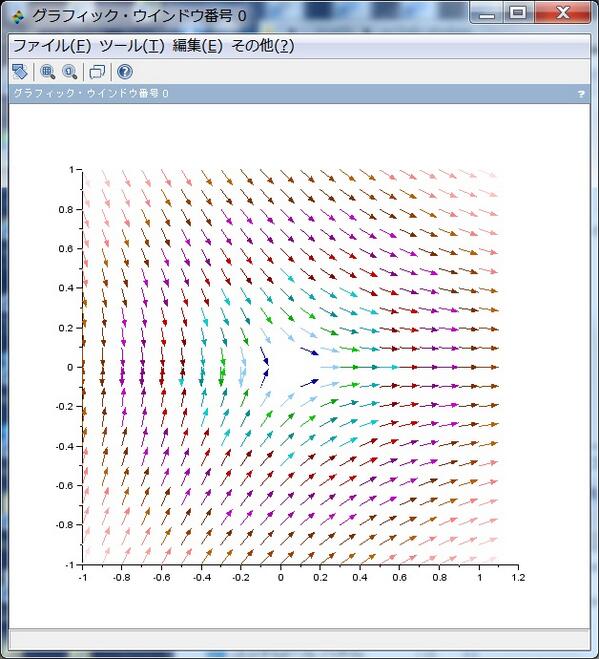
以下、√(Q(z)) の((実部),-(虚部))をプロットしたベクトル場と∫√(Q(z))dz の虚部の等高線をプロットしたものを放流。平方根の分岐がもろに見えちゃうので注意。Q(z)=z の場合のベクトル場。pic.twitter.com/O7mDWSx2VD
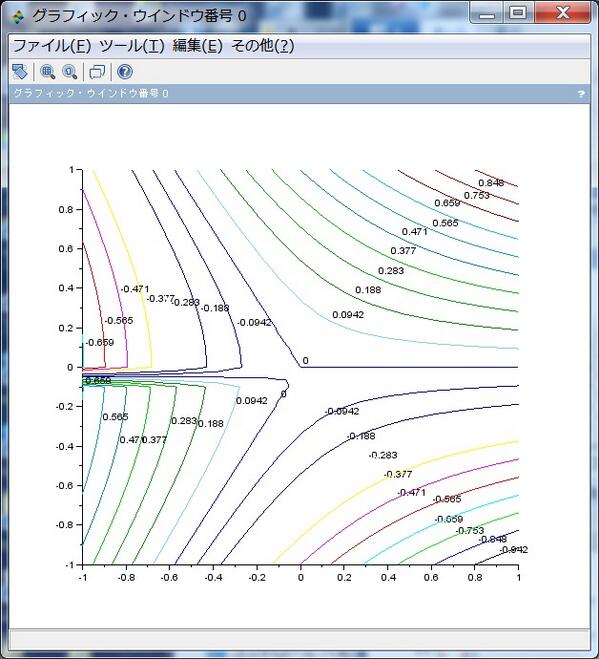
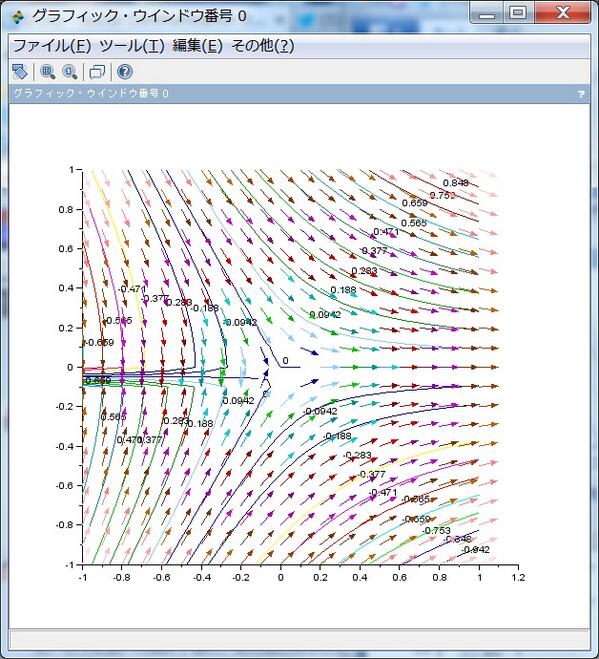
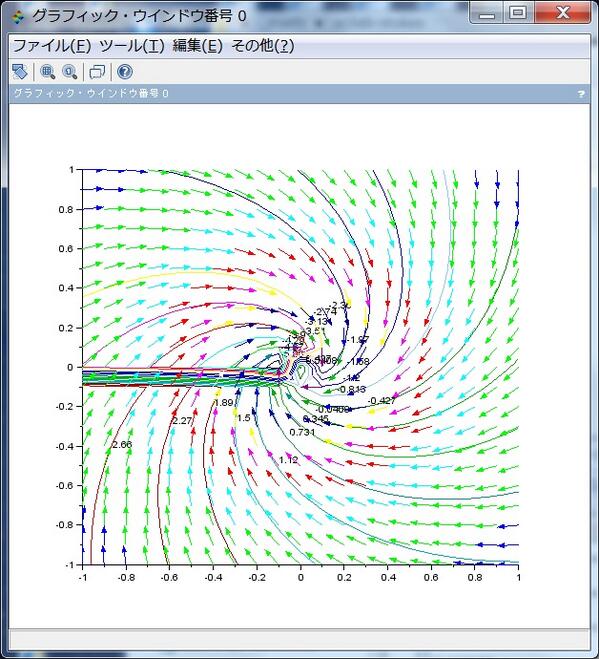
続き。double pole Q=((-1+i)/z)^2 の場合の √Q=(-1+i)/z のベクトル場とその不定積分の虚部の等高線を重ねたもの。 これについては面倒なので重ねてプロットしたものだけを放流。pic.twitter.com/in5Fs1GcFB
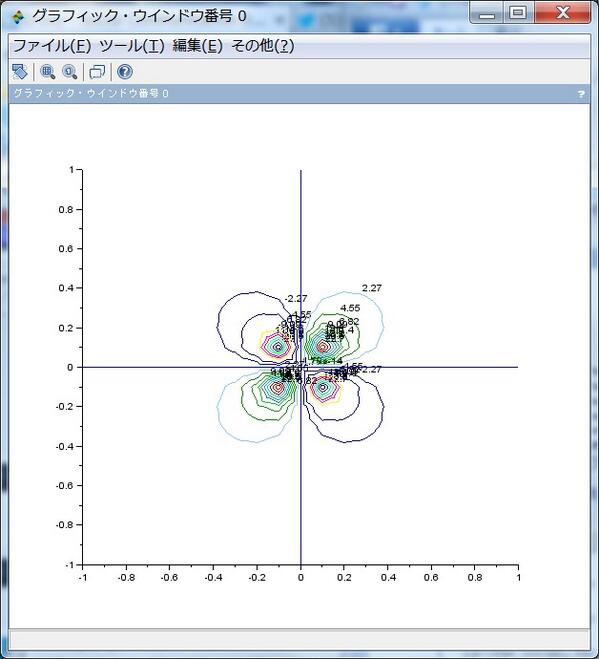
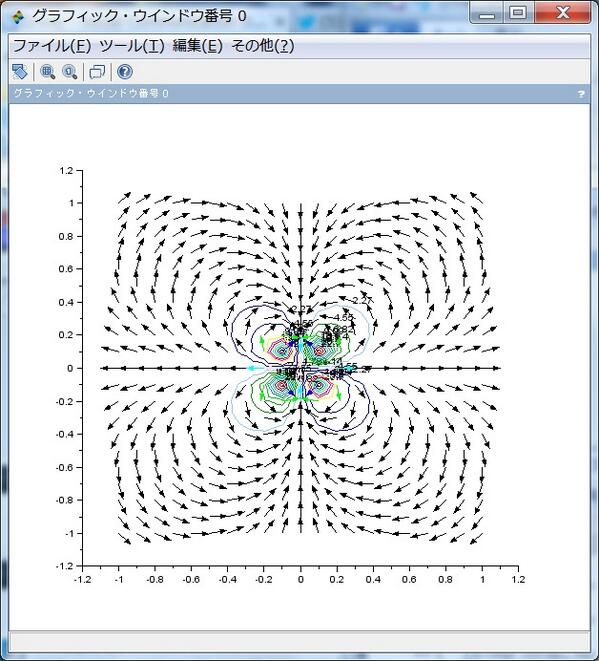
続き。6位の極 Q=1/z^6 の場合の √Q=1/z^3 で表わされるベクトル場とその不定積分の虚部の等高線を重ねてプロットしたもの。pic.twitter.com/BE53diNsmw
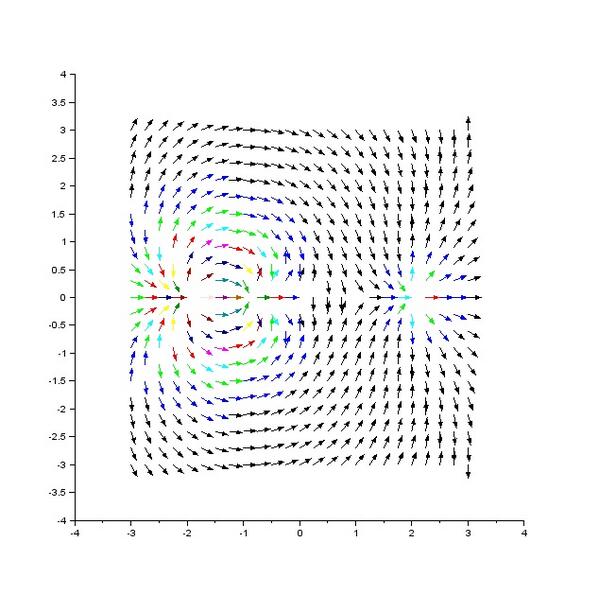
続き。Q=z(z-1)/((z+1)(z+2)(z-2))^2 の場合の√Q で表わされるベクトル場をプロットしたもの。面倒なのでこれについてはベクトル場のみを放流。pic.twitter.com/g0uIyDZvaW
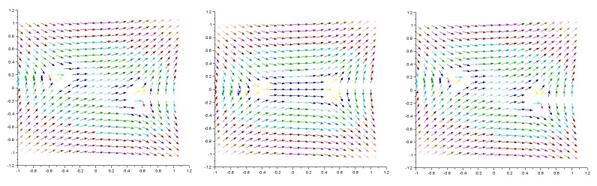
続き。Q=0.5^2+εi-z^2 で左から右にそれぞれε=-0.2,0,0.2 の場合の √Q のベクトル場の様子。pic.twitter.com/5XvLNGoEXl
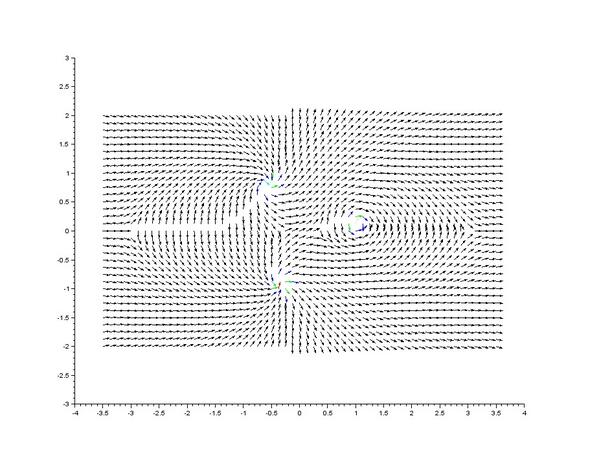
続き。これで最後。 Q=(z^2-9)(z^2-1/9)/(z^3-c)^2、 c=exp(πi/8) の場合の √Q で表わされるベクトル場の様子。河合・竹井『特異摂動の代数解析学』のp.50、図3.1と比較。pic.twitter.com/4d5C6ryyEZ
続き。ベクトル場のベクトルの長さは色で表示されているが、残念ながら、最後の奴はちょっとしか色がついてなくて分かり難い。使ったソフトは無料で誰でも使える scilab です。プロットの方法は https://twitter.com/genkuroki/status/439586730295828480 … 以降の連ツイに書いてある。以上です。
数学の話の続き。[DDP1993]第3節にペンタゴン恒等式が書いてあるという話が Kontsevich-Soibelman http://arxiv.org/abs/0910.4315 第7.5節に書いてあって、確かに書いてあるなあ。(cf. http://arxiv.org/abs/1401.7094 )
続き。しかも[DDP1993]は誰でもダウンロードできるっぽいし https://eudml.org/doc/74986 。数学の場合には高価な実験設備がいらないから、論文がダウンロードできると本当に誰でも正しさを確認できる(原理的には)。ただし仏語です。

続き。確かにDDP1993 https://eudml.org/doc/74986 のp.177にもろにpentagon identityが書いてあるよなあ。 誰がどう見てもこれはペンタゴン恒等式だ。pic.twitter.com/YKvSCdoWlC
数学話続き。この手の話は正準量子化ができてしかるべきだと思うのだが、そういうことはすでに知られていたりするのだろうか?量子二重対数が出て来る話がすでにないとおかしい感じがします。というようなことを考えながら玩具(scilabのこと)で遊んでいました。
数学話続き。DDP1993 https://eudml.org/doc/74986 のSection 3の内容が正準量子化されるということは、量子化される前のDDP1993の段階でポアソン構造が見えていないとおかしいんだよね。そこら辺はどうなっているんだろうか?
数学話続き。量子クラスター代数での"y変数"の非可換性(q可換性)の入れ方はHasegawa http://arxiv.org/abs/math/0703036 … での量子化されたq差分版のWeyl群双有理作用の場合と同じ。クラスター変換ではGCMが変化するが、Weyl群作用ではもちろん不変。
続き。さりげなく自分たちの仕事を紹介してみたりする。しかし、一つ前のツイートのケースでは量子τ変数なるものはまだ構成できていない。できているのは http://arxiv.org/abs/1206.3419 の場合。
続き。量子二重対数のペンタゴン恒等式は有名だが、q-Serre関係式に関係しているヘキサゴン恒等式があって、それが「q可換な場合」に退化することによってペンタゴンになっていると考えることもできる。q可換性はq-Serre関係式の十分条件になっている。
続き。q可換性とはYX=qXYのような関係式のこと。この条件はA_2型のq-Serre関係式 X^2Y-(q+1/q)XYX+YX^2=0の十分条件になっている。より高次のq-Serre関係式についても同様。
続き。量子展開環の普遍R行列の量子二重対数による表意についてはたとえばChari-Pressleyの第8節に書いてある。ただし有限型の場合。アフィン型では虚ルートがあるのでかなり面倒になる。普遍R行列の「実ルート因子」は量子二重対数で書ける。結構有名な話。



